Sampling Proportions and Means
| Topic Review on "Title": |
Rules for Sample proportion: The actual population must have fixed proportions that have a certain characteristics. If sampled over and over again from such proportion, a certain outcome is likely to occur with fixed probability.
Randomness and Independence:
- Random sample: each sample unit has equal opportunity of being selected.
- Independence: the same situation repeated numerous times, with outcome each time independent of all other times.
Large sample size: sample size needs to be sufficiently large.
Central Limit Theorem
- When large samples (≥30) of the same size are taken, the frequency curve made from proportions from various samples can be approximated by normal distribution.
- If we let p = true population proportion
- n =sample size
- We will have Mean=p
- Standard deviation =
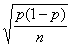
Rules and formula for Sample means: Population is approximately normal, and
Sample of size 30 is considered “large,” (larger sample is recommended if outliers are significant).
- Take random sample of any size.
- If population is not normal, take large random sample and apply Central Limit Theorem.
- If numerous samples of the same size are taken, the frequency curve of means from various samples will be approximately normal
- Mean will be same as mean for the population.
- Let σ= population standard deviation, n = sample size
- Standard deviation =
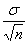
|
| Rapid Study Kit for "Title": |
| Flash Movie |
Flash Game |
Flash Card |
| Core Concept Tutorial |
Problem Solving Drill |
Review Cheat Sheet |
 |
 |
 |
|
| "Title" Tutorial Summary : |
This tutorial specifically describes the concepts of sampling proportions and means. By completing this course, you will learn about the sample proportions and means, including Sample proportions, Sample vs. proportions, Rules for sample proportions, Formula for sample proportions, Sample means, Rules for Sample Mean and Categorical Data.
Many examples are provided in the tutorial on rules and definition for sampling proportions and means. Formula for calculation and corresponding examples are also presented. In addition, categorical data is also discussed along with central limit theorem for practical application.
|
| Tutorial Features: |
Specific Tutorial Features:
- Numerical example showing the sampling proportions and means are provided.
- Step by step analysis from deciding a sampling proportion to calculating the statistics and then to normal approximation for practical application is presented.
Series Features:
- Concept map showing inter-connections of new concepts in this tutorial and those previously introduced.
- Definition slides introduce terms as they are needed.
- Visual representation of concepts
- Animated examples—worked out step by step
- A concise summary is given at the conclusion of the tutorial.
|
| "Title" Topic List: |
- Sample proportions
- Sample vs. proportions
- Rules for sample proportions
- Formula for sample proportions
- Sample means
- Rules for Sample Mean
- Categorical Data
|
See all 24 lessons in Introductory Statistics, including concept tutorials, problem drills and cheat sheets:
Teach Yourself Introductory Statistics Visually in 24 Hours |



