Discrete and Continuous Random Variables
| Topic Review on "Title": |
- Random Variables: A variable x is a random variable if the value that it assumes, is a numerical outcome of a random phenomenon or an experiment.
- Discrete Random Variables: A discrete random variable categorizes persons, objects, or events according to the kind or quality of their characteristics.
- Binomial random variable: a random variable that counts the number of successes in a sequence of independent Bernoulli trials with fixed probability of success.( Bernoulli trial refers to the two outcomes as success and failure).
- Poisson random variable: The probability that a certain number of random events occur in a given space of time (distance, etc.), can be calculated using the Poisson probability distribution, provided that certain conditions hold.
- Continuous random variables: A continuous random variable can take on infinite number of possible numerical values and are usually measurements.
- Probability distribution: the assignment of probabilities (p(x)) to the values of random variable x
- Normal random variable: The most important kind of continuous random variable
- Uniform random variable: The values of a uniform random variable are uniformly distributed over an interval.
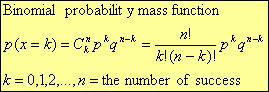
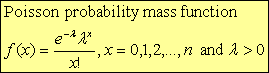
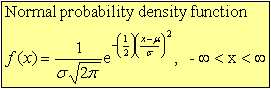
- Binomial
- Mean μ=np
- Variance σ2=npq
- Standard Deviation σ=√(npq)
- Poisson:
- Mean=λ
- Variance=λ
- Standar deviation=√λ
- Normal :
- Mean=μ
- Variance=σ2
- Standard deviation=σ
|
| Rapid Study Kit for "Title": |
| Flash Movie |
Flash Game |
Flash Card |
| Core Concept Tutorial |
Problem Solving Drill |
Review Cheat Sheet |
 |
 |
 |
|
| "Title" Tutorial Summary : |
The properties of discrete and continuous random variables are defined and used in the examples of this tutorial. By completing this tutorial, you will understand the properties of discrete random variables, binomial random variable, Poisson random variable, continuous random variables, normal random variable, uniform random variable and exponential random variable
In addition, the tutorial also shows you how to standardize the normal distribution and define the central theorem by using very illustrative examples.
|
| Tutorial Features: |
Specific Tutorial Features:
- Step by step examples are shown to describe the properties of discrete and random variables.
- Examples and graphs together make the operation of different random variables easy to understand.
Series Features:
- Concept map showing inter-connections of new concepts in this tutorial and those previously introduced.
- Definition slides introduce terms as they are needed.
- Visual representation of concepts
- Animated examples—worked out step by step
- A concise summary is given at the conclusion of the tutorial.
|
| "Title" Topic List: |
- Random Variables
- Discrete Random Variables
- Binomial random variable
- Poisson random variable
- Continuous random variables
- Probability distribution
- Normal random variable
- Uniform random variable
|
See all 24 lessons in Introductory Statistics, including concept tutorials, problem drills and cheat sheets:
Teach Yourself Introductory Statistics Visually in 24 Hours |



