Exponential Functions, Graphs and Models
| Topic Review on "Title": |
Domain of f(x):
The domain of 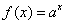 consists of all real numbers. consists of all real numbers.
Range of f(x):
The range of 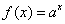 is the collection of all positive real numbers. is the collection of all positive real numbers.
Properties of exponentials:
1) 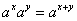
2) 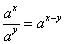
3) 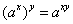
4) 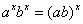
Increasing exponential function:
If 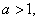 then then 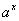 is an increasing function. is an increasing function.
Decreasing function:
If 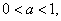 then then 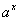 is a decreasing function. is a decreasing function.
|
| Rapid Study Kit for "Title": |
| Flash Movie |
Flash Game |
Flash Card |
| Core Concept Tutorial |
Problem Solving Drill |
Review Cheat Sheet |
 |
 |
 |
|
| "Title" Tutorial Summary : |
Exponential functions are one of the most important functions in mathematics. Exponentials are used in solving application problems such as population growth and decay .The operations of exponential functions are defined and used in the examples from this tutorial. The graph of an exponential function shows the exponential function properties that are used in commonly seen problems.
Euler’s number known as “e” is a famous one that is used in commonly based exponential problems. Basic exponential functions are shown with the use of examples and visual diagrams.
|
| Tutorial Features: |
Specific Tutorial Features:
• Step by step examples are shown to describe exponentials and how their properties are used to effectively show the effectiveness of them.
• Solving exponential functions are presented with the use of problem solving techniques.
Series Features:
• Concept map showing inter-connections of new concepts in this tutorial and those previously introduced.
• Definition slides introduce terms as they are needed.
• Visual representation of concepts
• Animated examples—worked out step by step
• A concise summary is given at the conclusion of the tutorial
|
| "Title" Topic List: |
Exponential functions and their definitions
Exponential functions and their properties
Exponential function graphs
Euler’s number and its definition
Exponential functions and their samples problems
|
See all 24 lessons in Trigonometry, including concept tutorials, problem drills and cheat sheets:
Teach Yourself Trigonometry Visually in 24 Hours |



