Inference with Proportions and Means
| Topic Review on "Title": |
- Inference: statistical inference is to perform testing and estimation in such a manner as to provide for the evaluation and control over the probabilities of making such errors.
- Tests of hypothesis: the statement about the values of population parameters may or may not be rejected.
- Estimation: the process by which sample data are used to indicate the value of an unknown quantity in the population.
- Experiment: data from a sample are used to test the validity of the hypothesis is called experiment.
- Statistical hypothesis: the hypothesis is stated in terms of population parameters such as the mean and variance.
- Null hypothesis: is a statement about the values of one or more parameters.
- Alternative hypothesis: the statement we hope or suspect is true.
- Type I error: null hypothesis is actually true but the decision is to reject it.
Level of significance maximum probability of committing a type I error.
- Confidence interval: certain probability that the true proportion is within the interval.
- Tests of significance: are used to assess the evidence provided by data in support of a claim about the population.
- P-value: the probability that the test statistic would take on as extreme a value as that observed, assuming that the null hypothesis is true.
Sample Mean
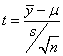
- Standard Deviation
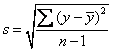
- Propotion p =
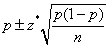
- Standard Error
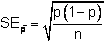
- Comparing proportions
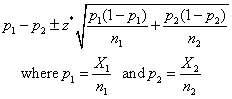
- Z Statistic
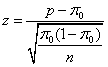
|
| Rapid Study Kit for "Title": |
| Flash Movie |
Flash Game |
Flash Card |
| Core Concept Tutorial |
Problem Solving Drill |
Review Cheat Sheet |
 |
 |
 |
|
| "Title" Tutorial Summary : |
Statistics is the art of decision making in the face of uncertainty. The field of statistical inference consists of those methods used to make decisions or draw conclusions about a population. These methods utilize the information contained in a sample from the population in drawing conclusions.
Tests of significance are used to assess the evidence provided by data in support of a claim about the population. The "strength of the evidence" against the claim is used to refute a false claim. Numerical examples are used to illustrate the steps in the hypothesis testing that leads to the final conclusion.
|
| Tutorial Features: |
Specific Tutorial Features:
- The properties of the inference with proportions and means are shown in the examples.
- Step by step explanation of hypothesis testing is provided.
Series Features:
- Concept map showing inter-connections of new concepts in this tutorial and those previously introduced.
- Definition slides introduce terms as they are needed.
- Visual representation of concepts
- Animated examples—worked out step by step
- A concise summary is given at the conclusion of the tutorial.
|
| "Title" Topic List: |
- Inference
- Test of hypothesis
- Type I and type II errors
- Inference on the population mean
- Confidence interval for proportions
- One population proportion hypothesis testing
- Comparing two population proportions
|
See all 24 lessons in Introductory Statistics, including concept tutorials, problem drills and cheat sheets:
Teach Yourself Introductory Statistics Visually in 24 Hours |



